Hui C.Y., Zhu B. and Ciccotti M., 2022. Finite deformation field near the tip of a Blatz–Ko wedge bonded to a rigid substrate. International Journal of Fracture, 238(1), 71-87.
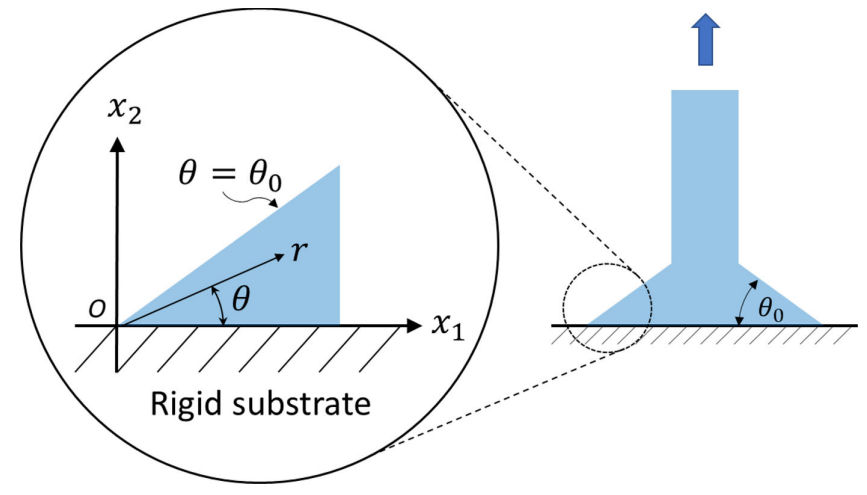
Sharp corners or wedges are common in everyday structures. Depending on the internal angle
theta0 of the wedge, severe stress concentration can occur. Linear elasticity predicts that when an incompressible elastic wedge is bonded to a rigid substrate and subjected to plane strain deformation, the stresses at the wedge tip has a power law singularity if theta > 44°. For some theta0 and for compressible wedges, the stresses are not only singular but oscillate infinitely rapidly. Here we show that these results are no longer true if large deformation is taken into consideration. Specifically, we determine the asymptotic fields near a tip of a Blatz–Ko wedge and found that the stress field has no power singularity for theta0 <= 90°. Furthermore, the power law singularity of the stress field differs from those predicted by linear elasticity and there are no oscillations. For sufficiently low compressibility, it is possible to obtain higher order terms of the asymptotic series—analogous to William’s expansion in linear theory. Our asymptotic results are validated by finite element calculations. We also studied the wedge tip field for the borderline case of a 90° wedge. For this case, the stress singularity is found to be at most logarithmic.


